Social Dilemmas - spatial effects:
Replicator updating
by Christoph Hauert, Version 1.0, November 2005.
- Location:
- VirtualLabs
- » Social Dilemmas
- » Structured populations
- » Replicator updating
Under replicator updating, a randomly selected focal individual compares its payoff to the payoffs of its neighbors (or a random sample of neighboring individuals) and adopts a neighboring strategy with a probability that depends on the payoff difference. If probability is proportional to the payoff difference, this updating rule recovers the replicator dynamics in the limit of infinite populations and large neighborhoods.
In the following scenarios, a focal individual with payoff Pf adopts the strategy of a model with payoff Pm that is randomly chosen among the neighbors of the focal individual with a probability proportional to Pm - Pf provided that the difference is positive and with probability zero otherwise.
Social Dilemmas
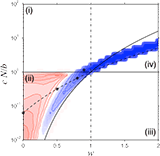
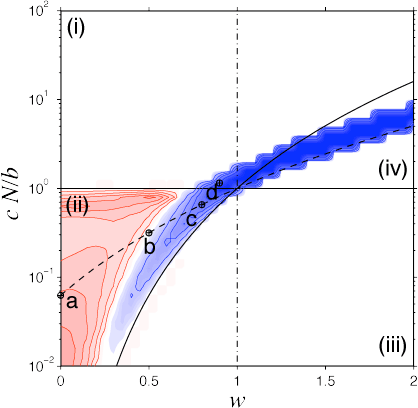
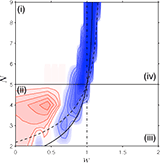
Space promotes cooperation in a small parameter range of region (i), i.e. in public goods type interactions where defection reigns in well-mixed populations. In bi-stable situations, region (iv), space increases the basin of attraction of the cooperative state because the threshold frequency of cooperation is much easier achieved locally than globally. Region (iii) where cooperation is dominant remains unaffected by spatial structure. However, the most interesting effects of space occur in region (ii) where cooperators and defectors co-exist in well-mixed populations. Here space may be beneficial but often it turns out to be deleterious and may even eliminate cooperation. The points d, a, b and c indicate the parameter settings of the first four sample scenarios listed below (in this order).
Social Dilemmas
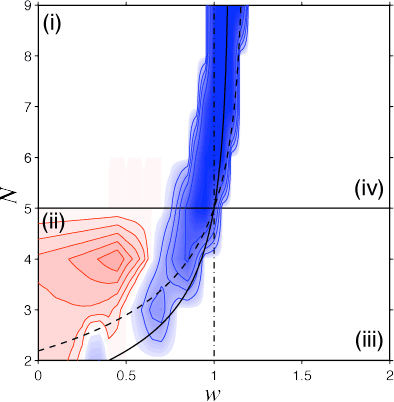
This view of the phase space confirms the positive effects of space on cooperation in regions (i) and (iv) while leaving region (iii) unaffected. In the region of co-existence (ii), spatial structure can again be beneficial but often limited local interactions are detrimental to cooperation. Note that the detrimental effects are most pronounced for replicator type updating of the players. For Moran type updating the parameter range where space inhibits cooperation is largely reduced and, in particular, for the death-birth variant detrimental effects are essentially eliminated.
  Click to enlarge Click to enlarge |
Spatial effects in social dilemmas: cooperation versus c N/b and wEffects of spatial structure on cooperators and defectors as compared to well-mixed populations. The change in equilibrium frequencies is shown for a fixed group size N = 5 and as a function of the normalized cost-to-benefit ratio c N/b and of the synergy/discount factor w. In blue regions space promotes cooperation and in red regions spatial structure reduces the equilibrium fraction of cooperators. The saturation of the colors indicates the strength of the effect. In well-mixed populations, defectors dominate in region (i) and cooperators dominate in region (iv). Along the dashed line, equal proportions of cooperators and defectors represent a fixed point, which is stable in region (ii), indicating co-existence of cooperators and defectors, but unstable in region (iv) separating the basins of attraction of the homogeneous states with all cooperators and all defectors, respectively (bi-stability). |
|---|---|
 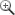 Click to enlarge Click to enlarge |
Spatial effetcs in social dilemmas: cooperation versus N and wSame situation as above but now the effects of space on the equilibrium fraction of cooperators are shown for a fixed cost-to-benefit ratio c/b = 0.2 and as a function of the group size N and of the synergy/discount factor w. For the replicator updating, spatial structure has pronounced effects on the equilibrium fraction of cooperators in both positive (regions (i), (iv) and parts of (ii)) and negative ways (parts of region (ii)). Compared to that, the effects of space are moderated for birth-death updating where the positive effects are less pronounced but, in particular, the detrimental effects of space are largely reduced. Conversely, for death-birth updating space has the most pronounced positive effects on cooperation and essentially eliminates the deleterious effects in region (ii). |
Scenarios
Clicking either on one of the pictures below (or the corresponding link to the right) opens a new window with a running applet with all parameters preset to illustrate the respective scenario. You can use this as a starting point to study effects of variations of the parameters.
Legend | Time evolution of cooperators and defectors in structured populations where individuals engage in social dilemmas.
| ||||||
|---|---|---|---|---|---|---|---|
 |
Region (i): public goods games (c N/b > 1, c N/b > wN-1)In public goods type interactions cooperators are doomed and vanish in well-mixed populations but spatial structure allows cooperators to survive by forming clusters and therbey reducing exploitation by defectors. The clustering advantages are limited but enables cooperators to persist in a small parameter region (see phase plane diagrams above). In comparison, birth-death updating supports fewer and death-birth updating much higher fractions of cooperators for the same parameter values. The figure on the left depicts a snapshot of a typical lattice configuration. | ||||||
 |
Region (ii): snowdrift games (1 > c N/b > wN-1)In snowdrift type interactions cooperators and defectors stably co-exist in well-mixed populations. Interestingly, in this case the effects of space, i.e. of limited local interactions and clustering opportunities need not be favorable for cooperation. While spatial settings can promote cooperation, they often actually inhibit cooperation as compared to well-mixed populations or even eliminate cooperation altogether. This and the next two scenarios illustrate the different effects of space in snowdrift type interactions. In all three cases cooperators and defectors co-exist with equal proportions in well-mixed populations. In the first scenario, the synergy/discount factor w is zero, the benefits b are rather high and the equilibrium fraction of cooperators is reduced to about 40%. The figure on the left shows a typical snapshot of the lattice configuration. | ||||||
 |
Region (ii): snowdrift gamesSame snowdrift type interactions as above but for larger w and smaller b such that the equilibrium fraction of cooperators remains 50% in well-mixed populations. In this case spatial structure does produce correlation patterns but leaves the fraction of cooperators essentially unaffected, as shown in a snapshot of a typical lattice configuration on the left. | ||||||
 |
Region (ii): snowdrift gamesFor the third scenario of snowdrift type interactions w is further increased and b is further decreased, keeping the equilibrium fraction of cooperators at 50% in well-mixed populations. In this last scenario spatial structure turns out to be beneficial for cooperation and defectors are reduced to small patches (see snapshot of a typical lattice configuration on the left). In snowdrift type interactions, the effects of spatial structure rather delicately depend on the update rule of the players. This is not so surprising because this update rule essentially determines the equilibrium correlations in the system. For Moran type updating (birth-death and death-birth processes) the detrimental effects of space are largely reduced. | ||||||
 |
Region (iii): by-product mutualism (c N/b < 1, c N/b < wN-1)In the case of by-product mutualism cooperation is the dominant solution and defectors disappear. Intriguingly, on average cooperators outperform defectors but in each interaction group defectors are better off than cooperators. Spatial structure does not affect this outcome and the system relaxes into a homogenous state with all cooperators. The different update rules, however, have significant effects on the time scale. The snapshot on the left depicts a typical lattice configuration of the transient phase after 50 generations with 5% cooperators initially. For the replicator updating the spreading speed is much slower than for birth-death and death-birth updating where cooperators occupy larger territory after 10 generations. | ||||||
 |
Region (iv): coordination games (1 < c N/b < wN-1)In coordination games the evolutionary end state depends on the initial configuration. In well-mixed populations cooperators thrive if their initial frequency is above a threshold and disappear otherwise. Spatial structure significantly enhance the basin of attraction of the cooperative state because this threshold no longer needs to be achieved on a global scale but rather only locally. After initialization, a sufficiently large cluster of cooperators can act as a seed and eventually take over the entire population. This means that locally the required abundace of cooperators can be quite easily satisfied which leads to such superiority of cooperators in the bi-stable regime. The evolutionary outcome now depends on the presence of a sufficiently large cluster of cooperators after initialization and thus not only depends on the initial fraction of cooperators (c.f. well-mixed populations) but also on the system size. The figure to the left illustrates a transient phase where several 'cluster-seeds' are expanding and eventually will cover the entire lattice. |